Table of Contents
1. Revision
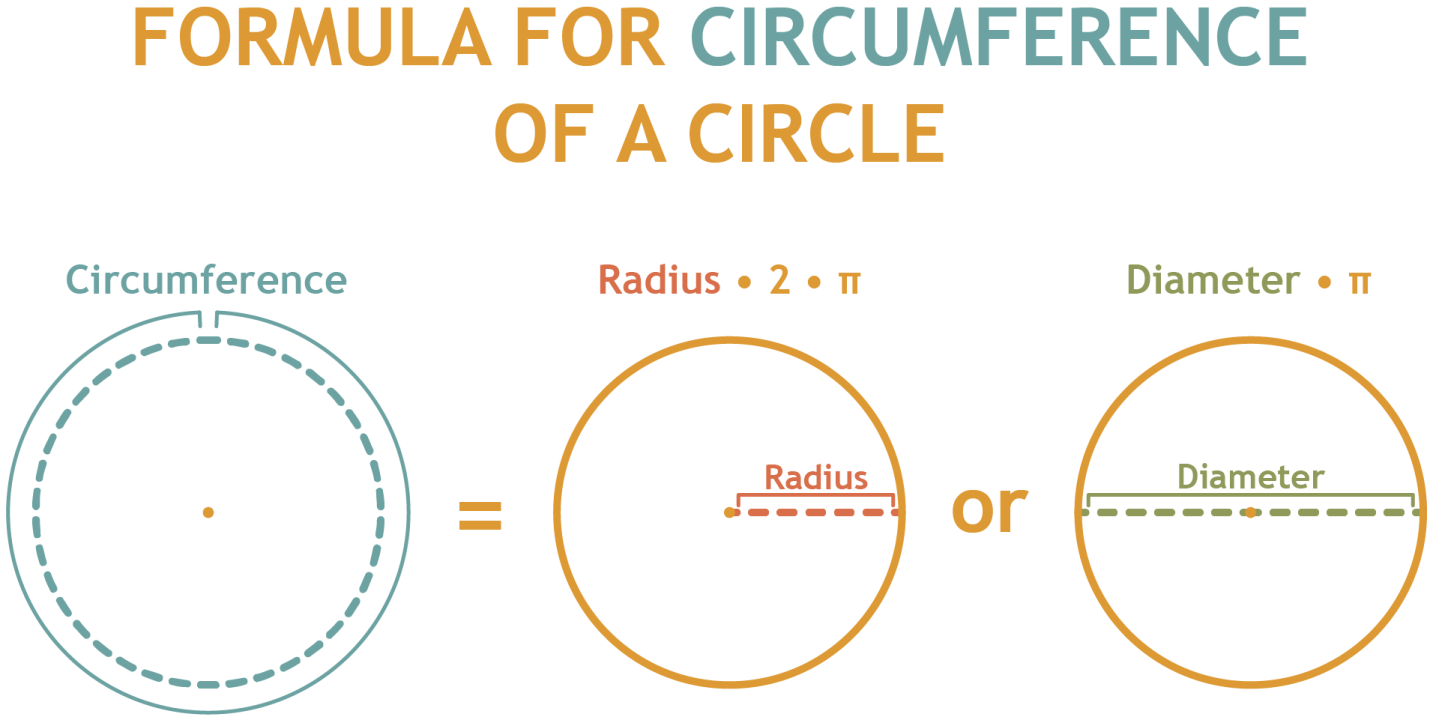
-Circumference of a circle = Radius•2•π
-The diameter is double the radius, so you could also say: Diameter•π
Legend
• = Multiplication
π = Pi
≈ = Approximately equal to
2. Unit circle
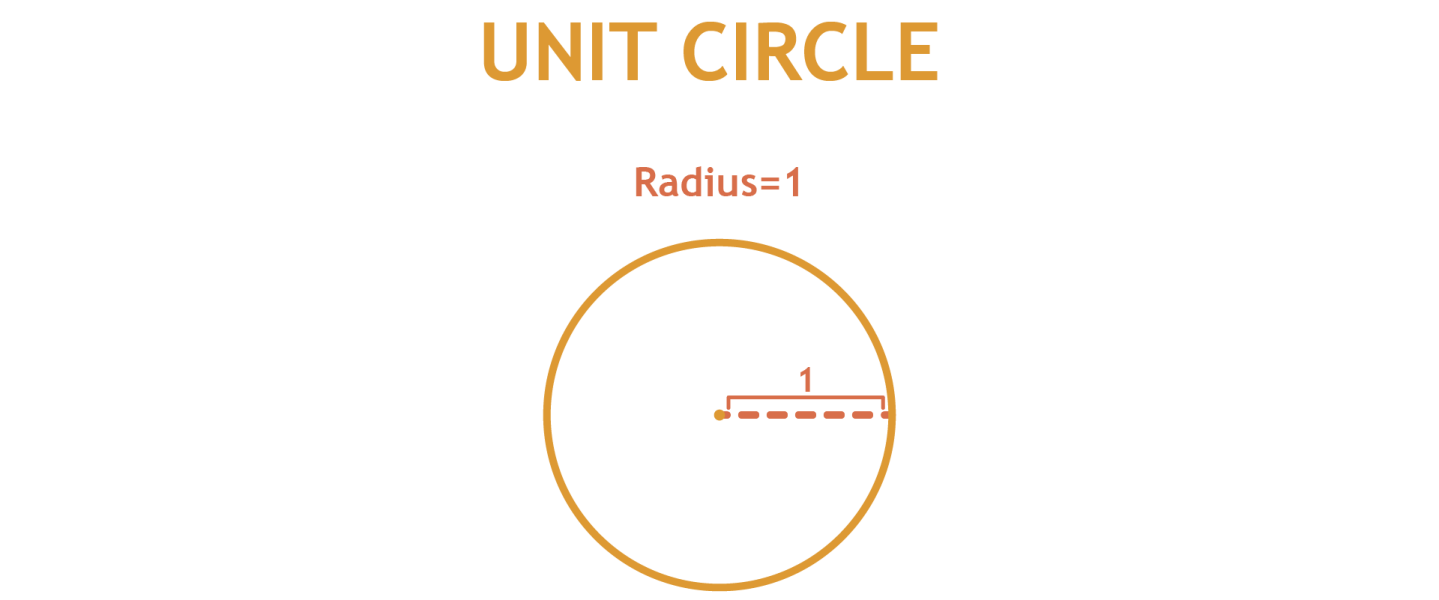
A unit circle is a circle with a radius of 1.
3. Arc
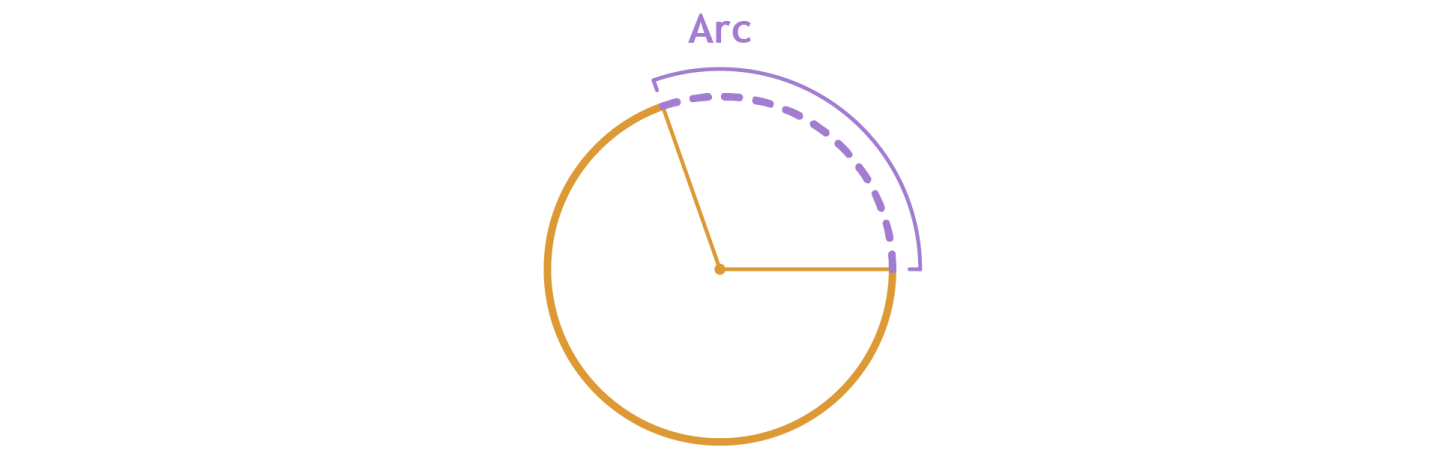
The arc is a part of the circumference of a circle.
4. Radian
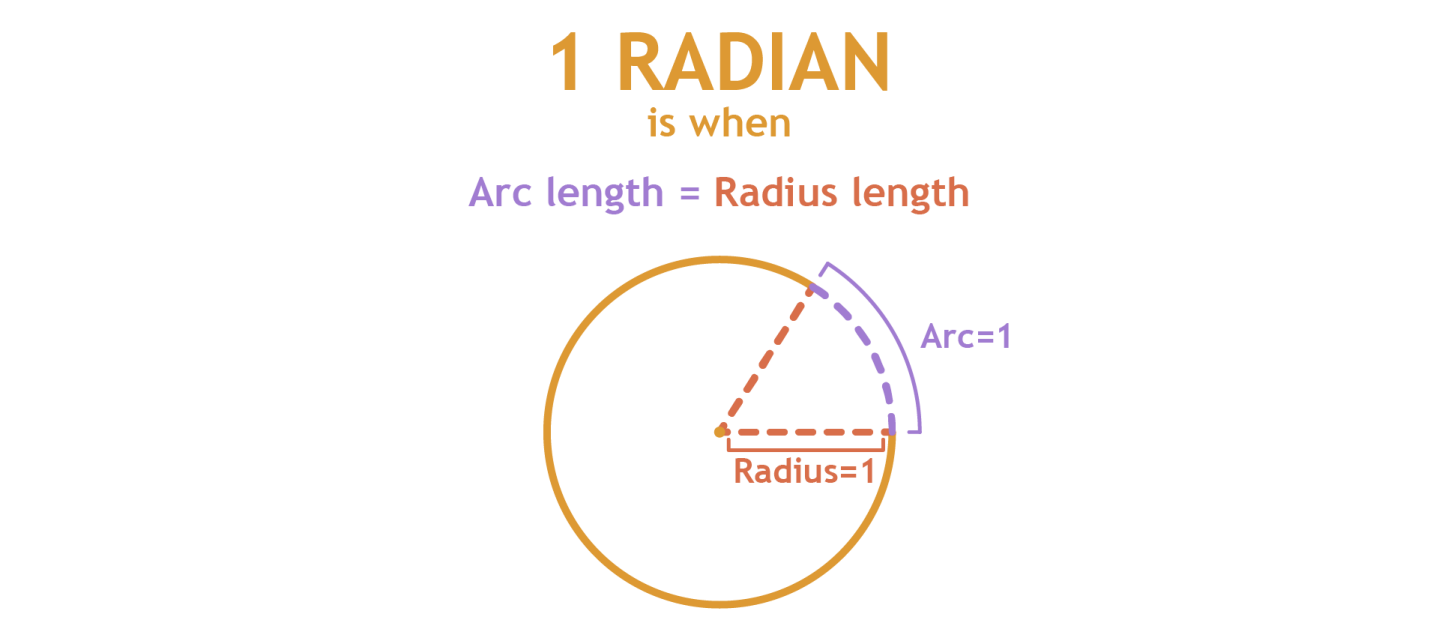
A radian is an arc that has the same length as the radius. We know that a unit circle has a radius length of 1. That means that for a unit circle 1 radian will have an arc with the length of 1.
5. Dividing a circle in radians
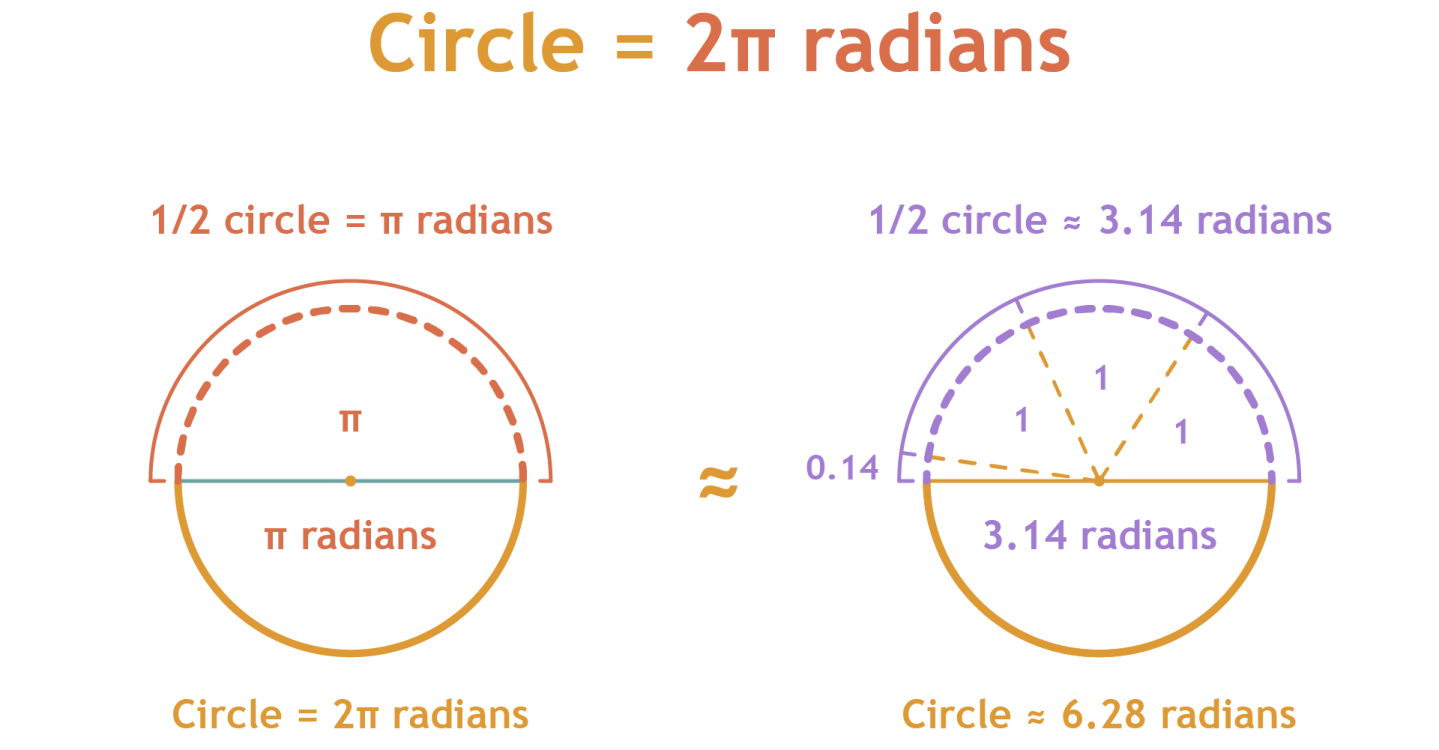
When you are dividing a circle in radians, about 3.14 radians will fit in each half of the circle. So a full circle fits about 6.28 radians. The exact amount of radians that fit in half a circle is π (which is about 3.14), so a full circle fits 2π radians (which is about 6.28).
6. Angle of π radians
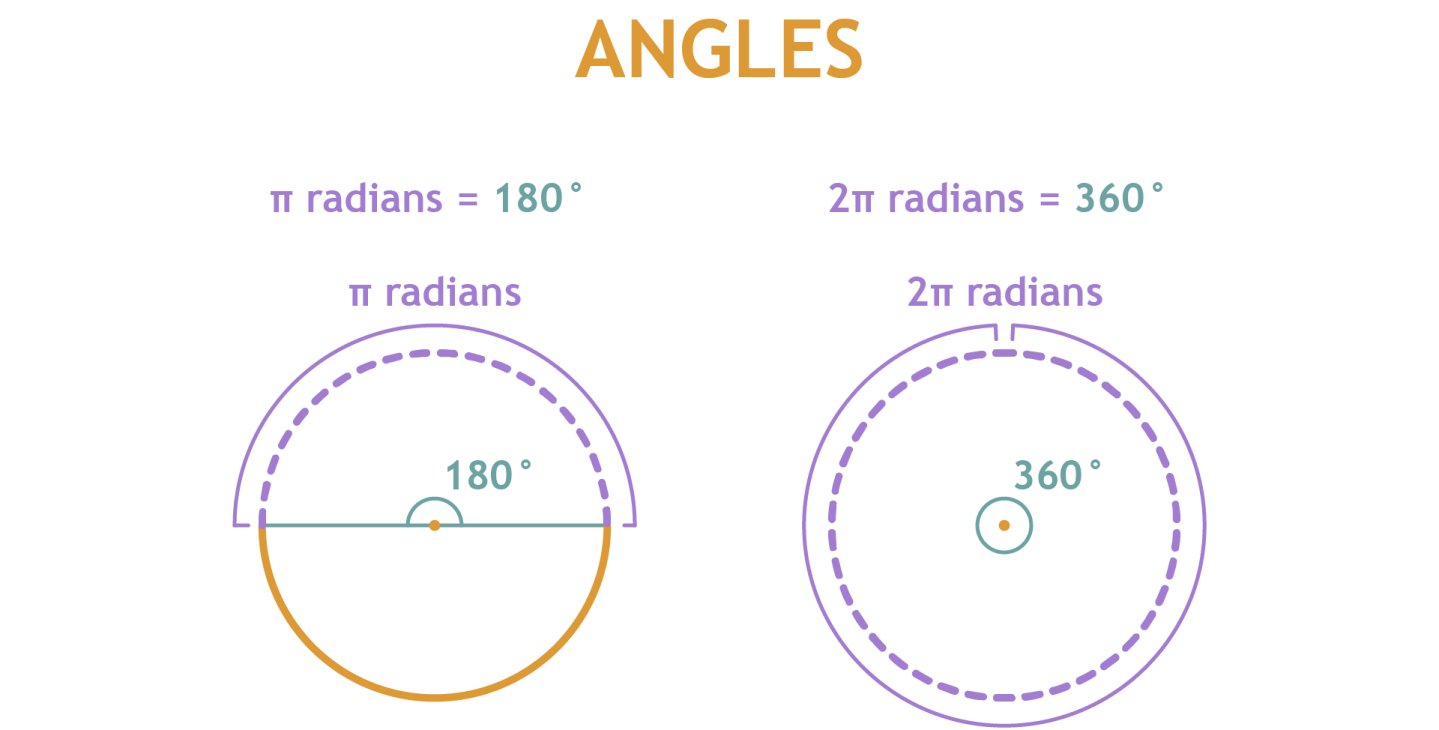
An angle of 180° is equal to a π amount of radians. This means that the amount of radians of a full circle equals to 2π. 2π therefore is 2•180° = 360°.
Calculating angles of radians
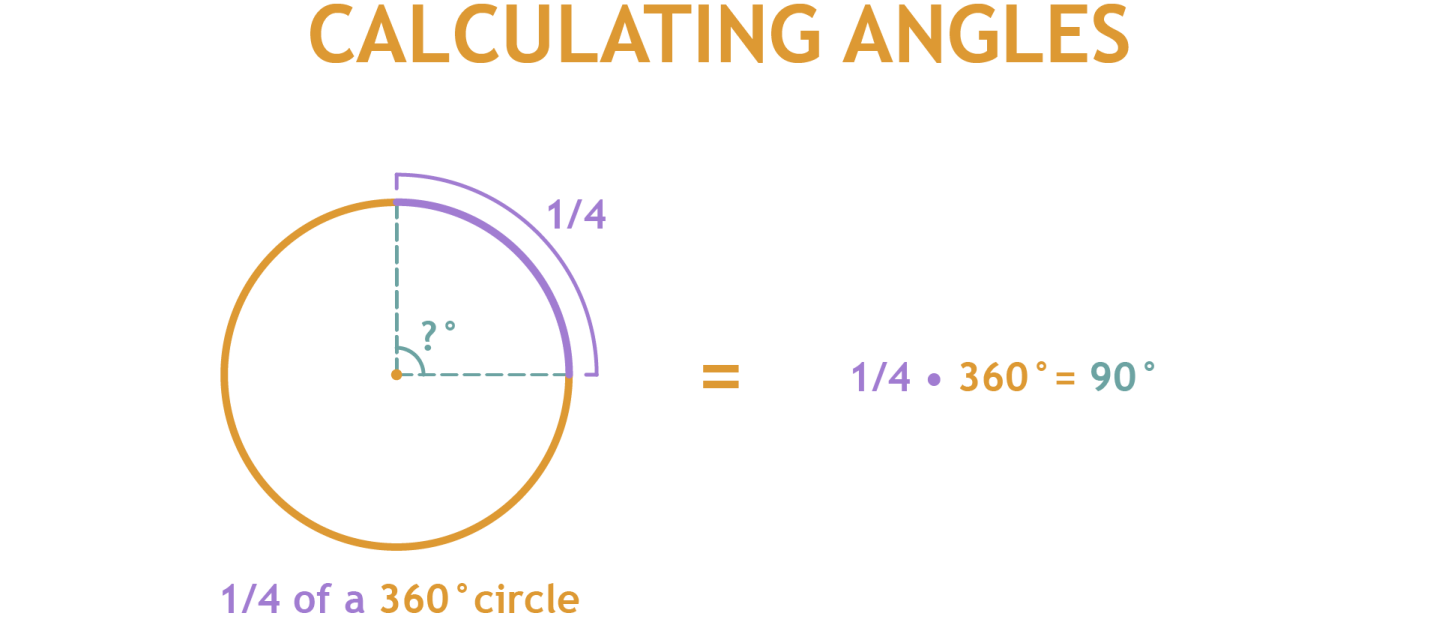
Lets first try something simple. For example a quarter of a circle. This is 1/4 part of the circle. 1/4 part of a 360° circle gives us the formula 1/4•360°. This gives us the solution of 90°.
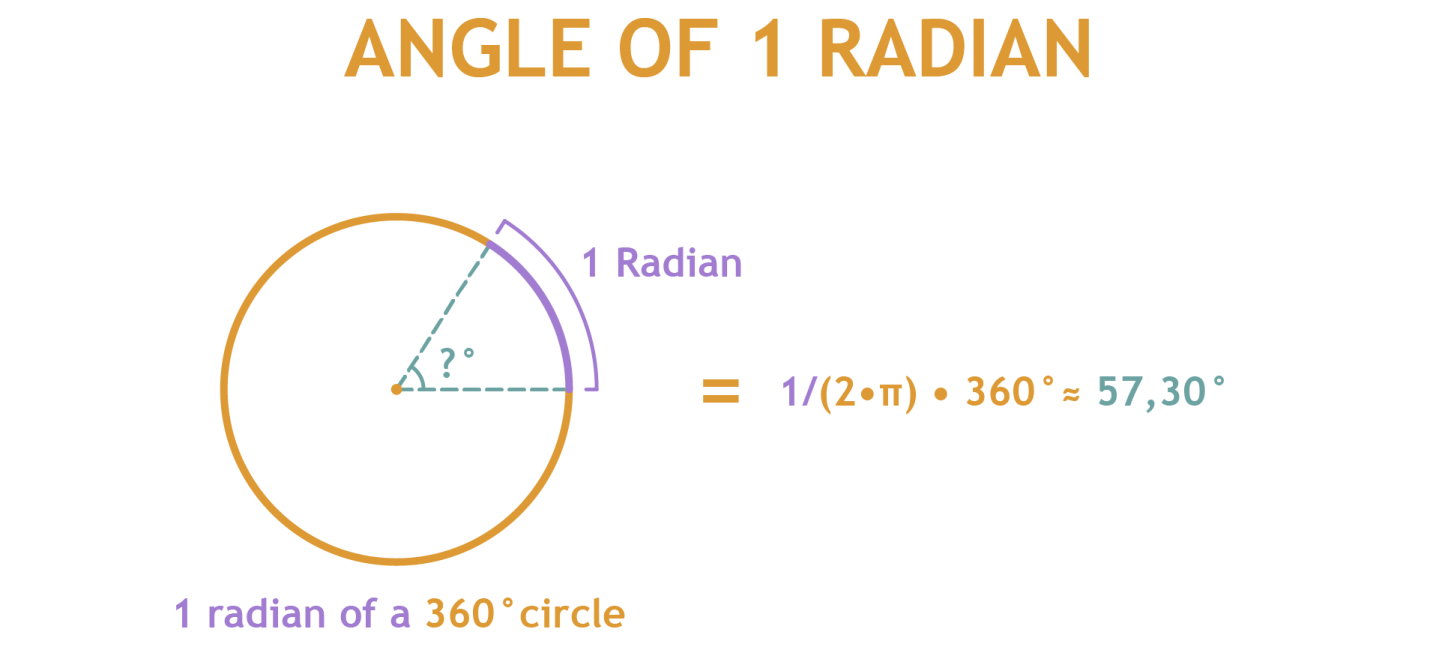
Now an angle of a radian. A circle consists of 2π radians (about 6.28 radians) which equals to 360°. What we want to know now is an 1/ 2π part of a circle (so actually about an 1/6.28 part). This gives us the formula 1/(2π)•360°. This gives us the solution of about 57.30°.
This can be done a bit more simple. Instead of calculating 1/2π part of a full circle, you could also calculate 1/π part of half a circle of 180°. Now when we calculate the angle of a radian we get the formula: 1/π•180°.
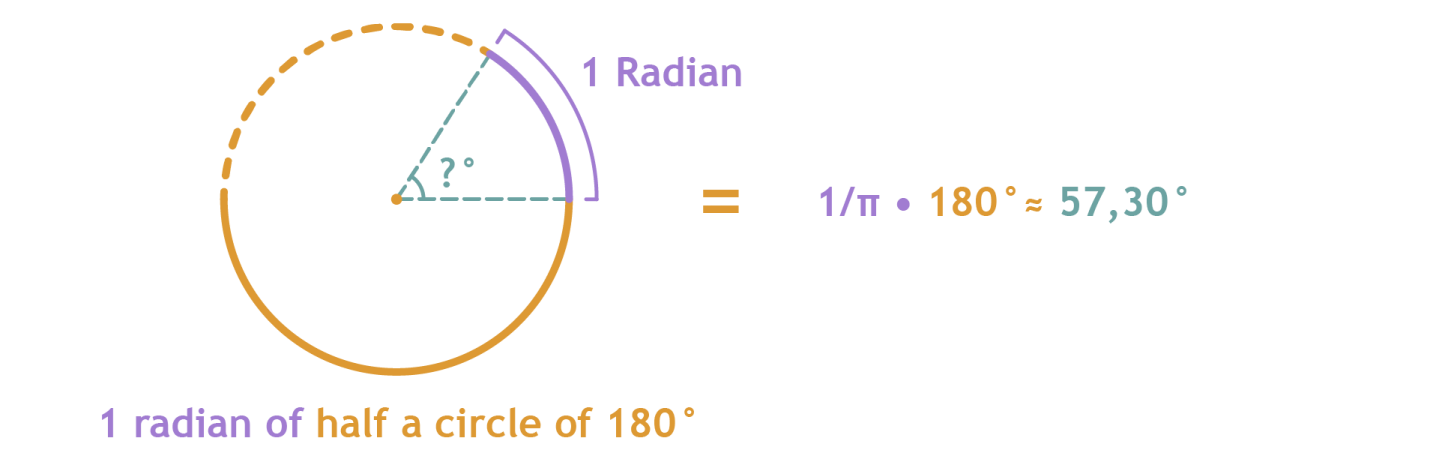
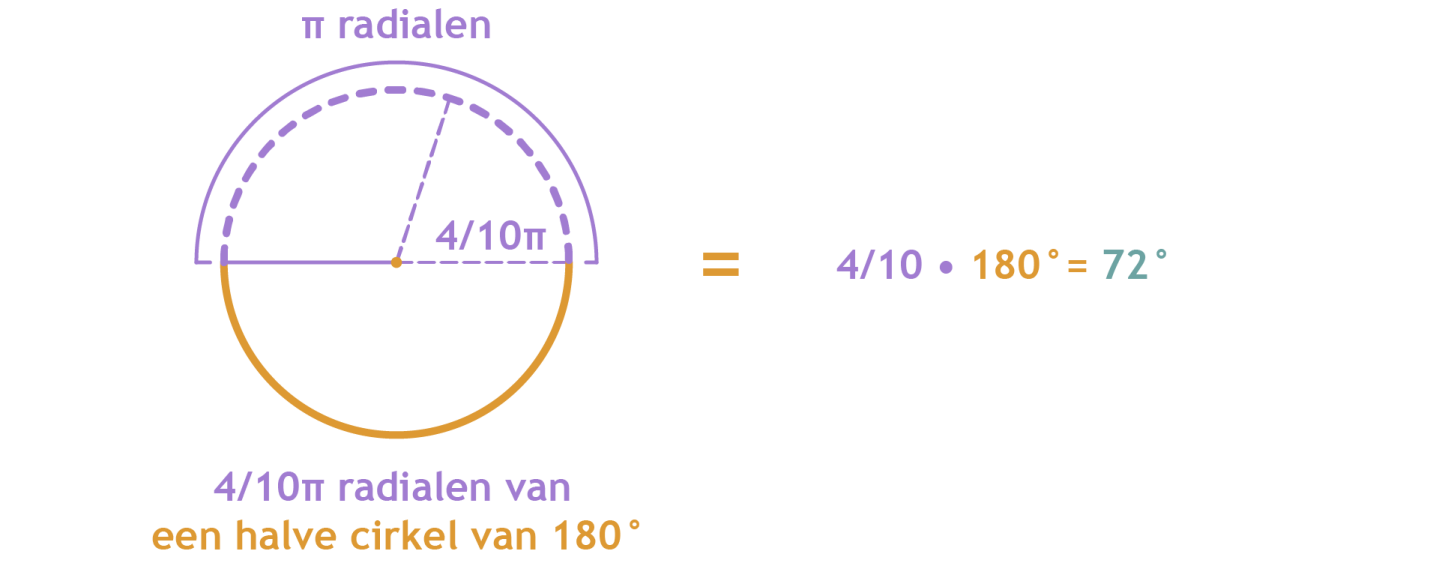
This works the same when you try to calculate the angle of 4/10π radians. 4/10π is actually 4/10 part of π. We now know that π equals to 180°. So what we want to calculate is 4/10 part of 180°. Then we get the formula: 4/10•180°. This gives us a solution of 72°.

7. In summary
The size of the angle of 1 radian is about 57.30°. In math we use this angle as measurement. We call this measurement a radian, instead of the angle. So when a radian is mentioned, it refers to an angle of about 57.30°. The abbreviation of a radian is “rad”. P.S. “π rad” isn’t pronounced “pirate”. 😉
The ratio, in a radian, between the arc and the radius is always the same, because the length of the arc in a radian is the same as the radius. This means that a circle always consists of 2π radians and that the angle of the radian will always be 57.30°. In every circle with whatever measurements.
In short a radian is an arc with a length that is equal to the length of the radius. And a radian always has an angle of about 57.30°.
8. Formulas
From angles to π rad:
45° = 45/180°•π = 1/4•π rad
From π rad to angles:
0.5π rad = 0.5•180° = 90°
From decimal rad to angles:
1.5 rad = 1.5•(180°/π) ≈ 86°
From angles to decimal rad:
86° = 86/180°•π ≈ 1.5 rad
1. Herhaling
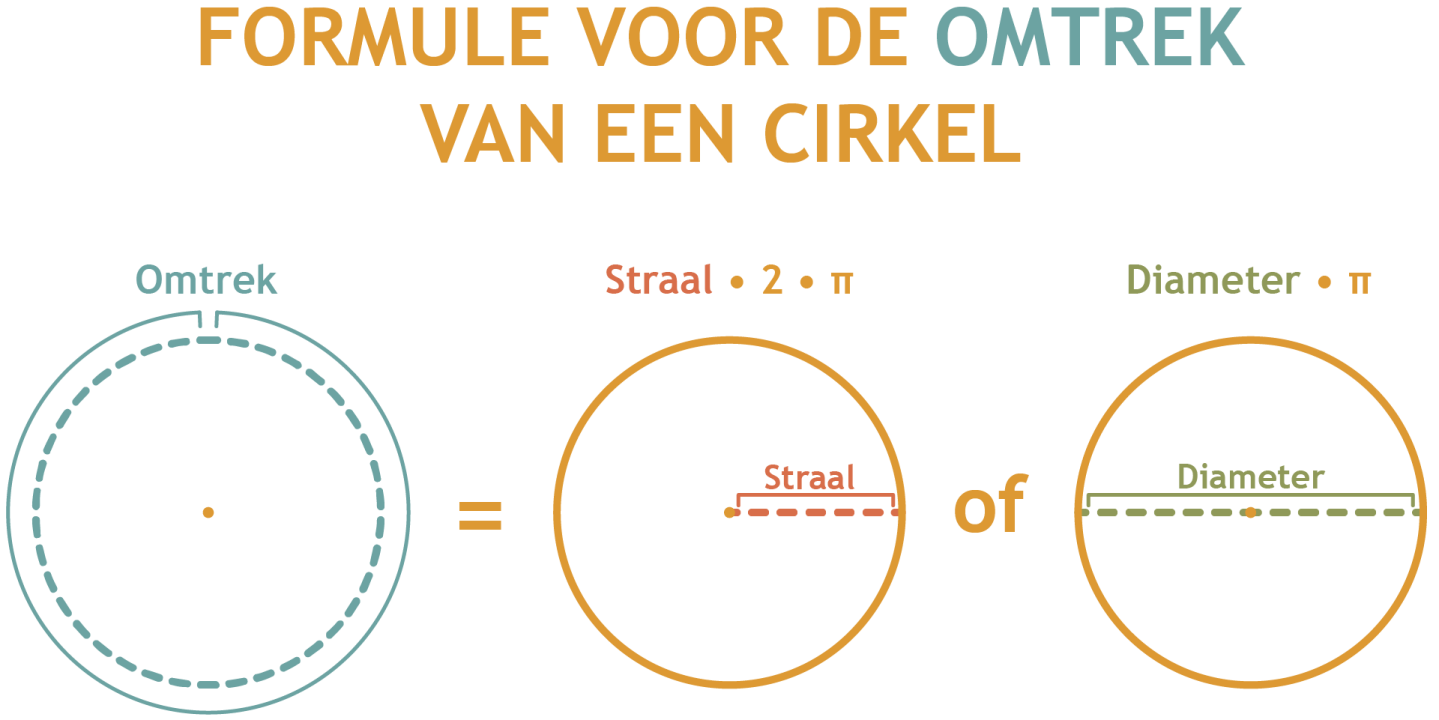
-Omtrek cirkel = Straal•2•π
-De diameter is het dubbele van de straal, dus je zou ook kunnen zeggen: Diameter•π
Legenda
• = Vermenigvuldigen
π = Pi
≈ = Ongeveer gelijk aan
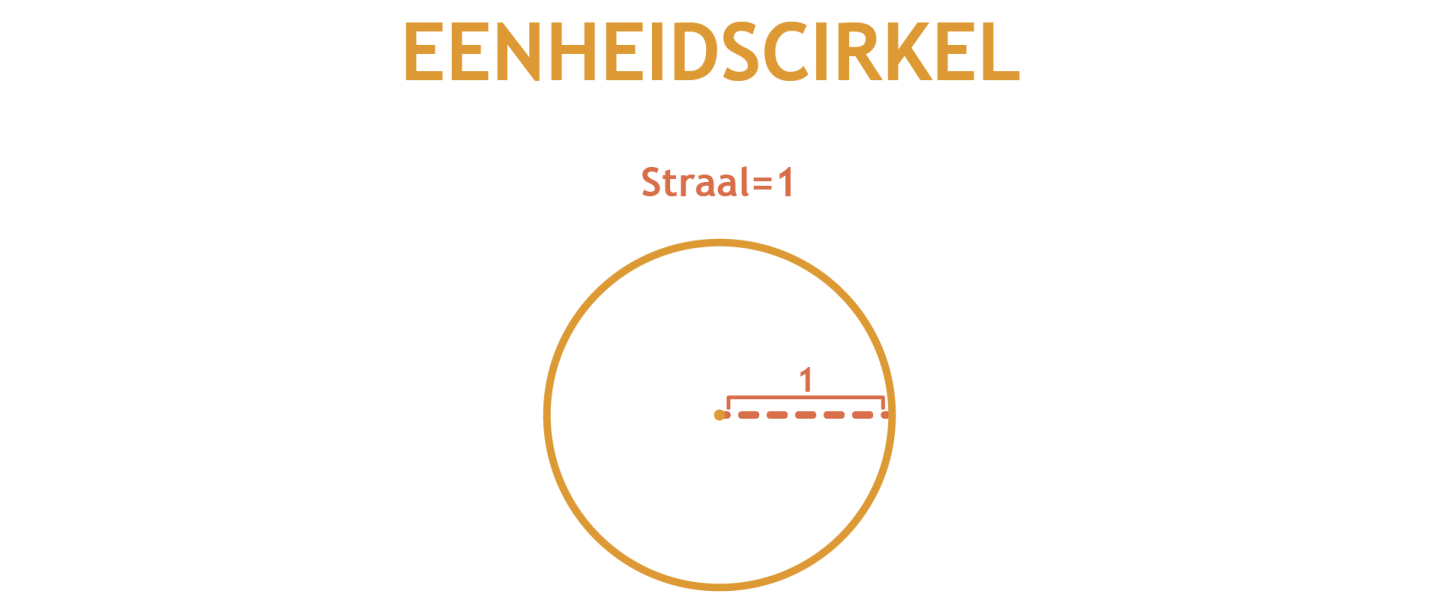
2. Eenheidscirkel
Een eenheidscirkel is een cirkel met een straal van 1.
3. Cirkelboog
De cirkelboog is een deel van de omtrek van de cirkel.

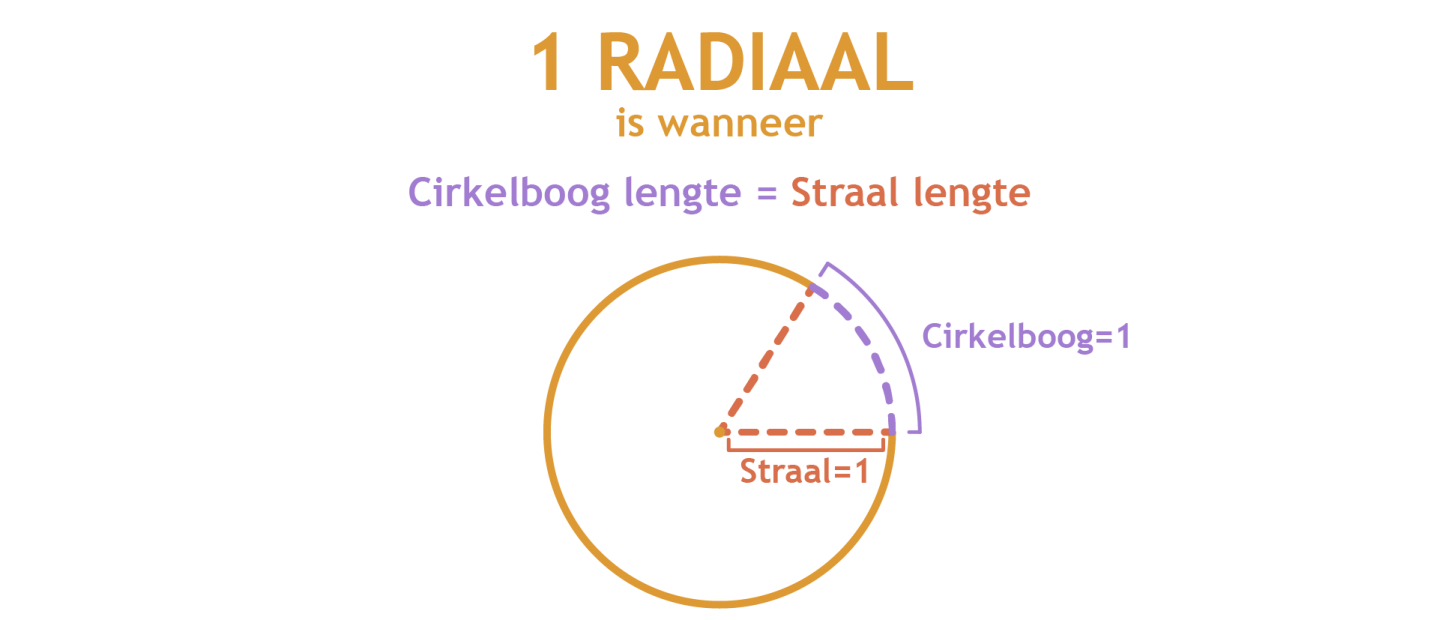
4. Radiaal
Een radiaal is een cirkelboog die dezelfde lengte heeft als de straal. We weten dat de straal van een eenheidscirkel de lengte 1 heeft. Dat betekent dat voor een eenheidscirkel 1 radiaal een cirkelboog heeft met de lengte 1.
5. Cirkel verdelen in radialen
Wanneer je een cirkel verdeelt in radialen past er in elke helft van de cirkel afgerond 3,14 radialen, dus in de gehele cirkel afgerond 6,28 radialen. Het precieze aantal radialen dat in een halve cirkel past is π (wat afgerond 3,14 is), dus in een gehele cirkel passen 2π radialen (wat afgerond 6,28 is).
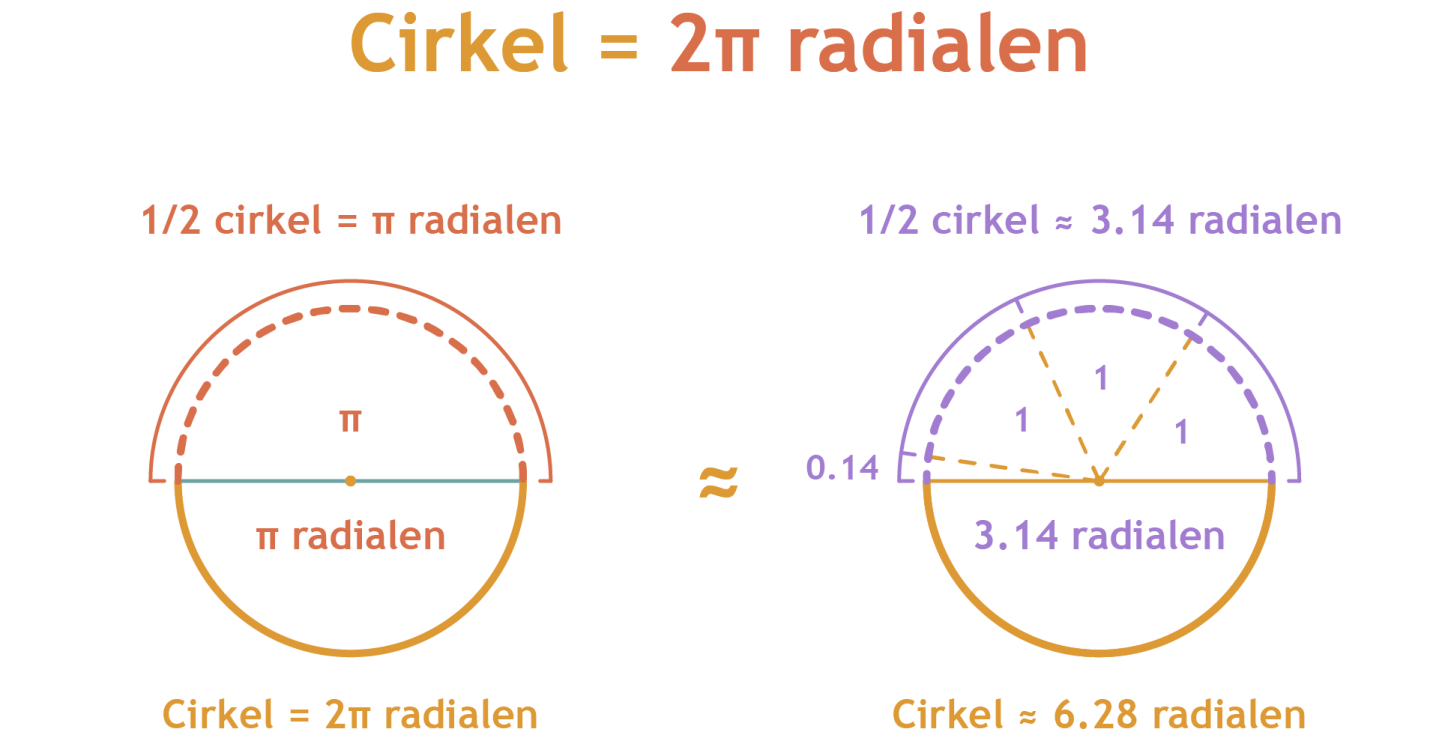
6. Hoek van π radialen
Een hoek van 180° komt overeen met een radialen aantal van π. Dit betekent dat het aantal radialen van de gehele cirkel gelijk is aan 2π. 2π is dan dus 2•180° = 360°.
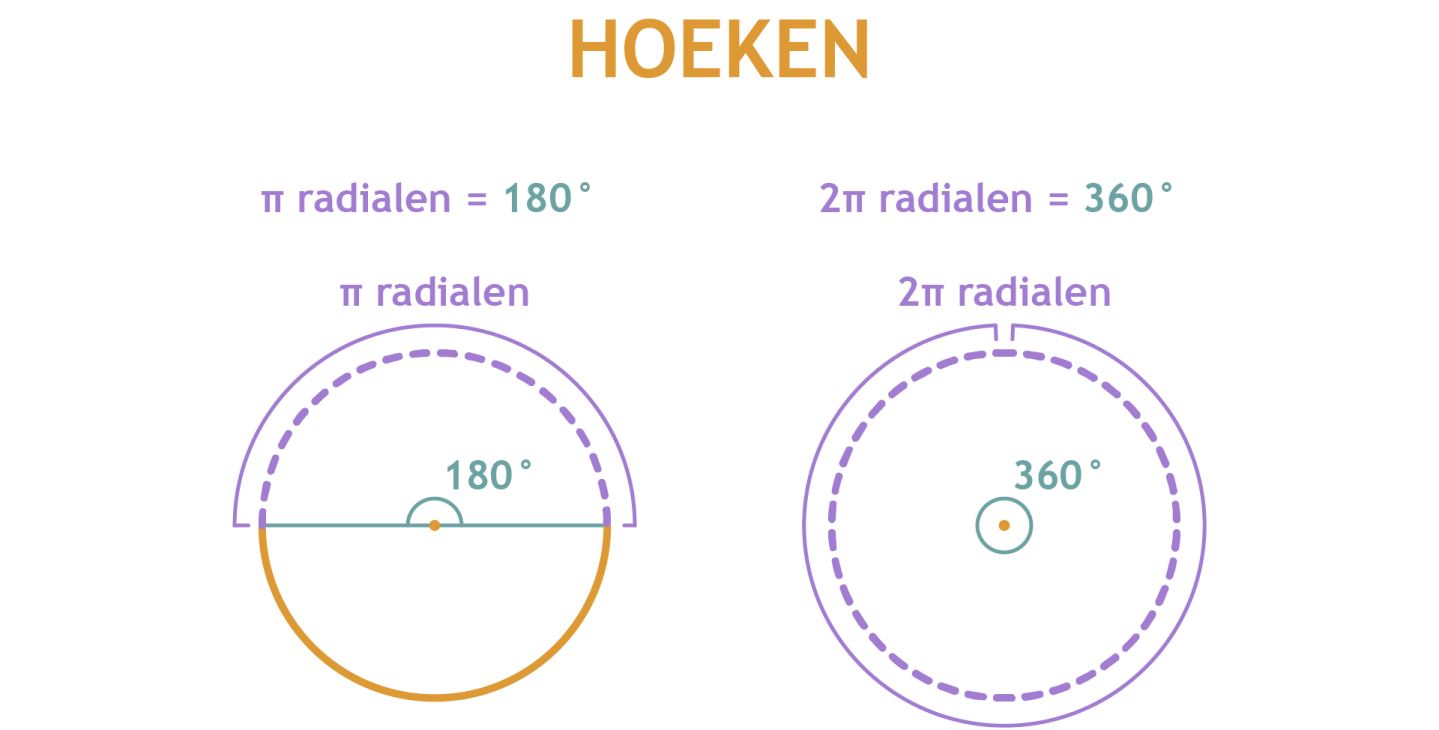
Hoeken van radialen berekenen
Laten we eerst een simpel voorbeeld nemen. Bijvoorbeeld een kwart van de cirkel. Dit is 1/4 deel van de cirkel. 1/4 van een 360° cirkel geeft de formule 1/4•360°. Dit geeft als oplossing 90°.

Dan nu een hoek van een radiaal. Een cirkel bestaat uit 2π radialen (afgerond 6,28 radialen) wat dus gelijk is aan 360°. We willen een 1/2π deel weten van de cirkel (dus eigenlijk afgerond een 1/6,28 deel). Dit geeft de formule 1/(2π)•360°. Dit geeft als oplossing afgerond 57,30°.
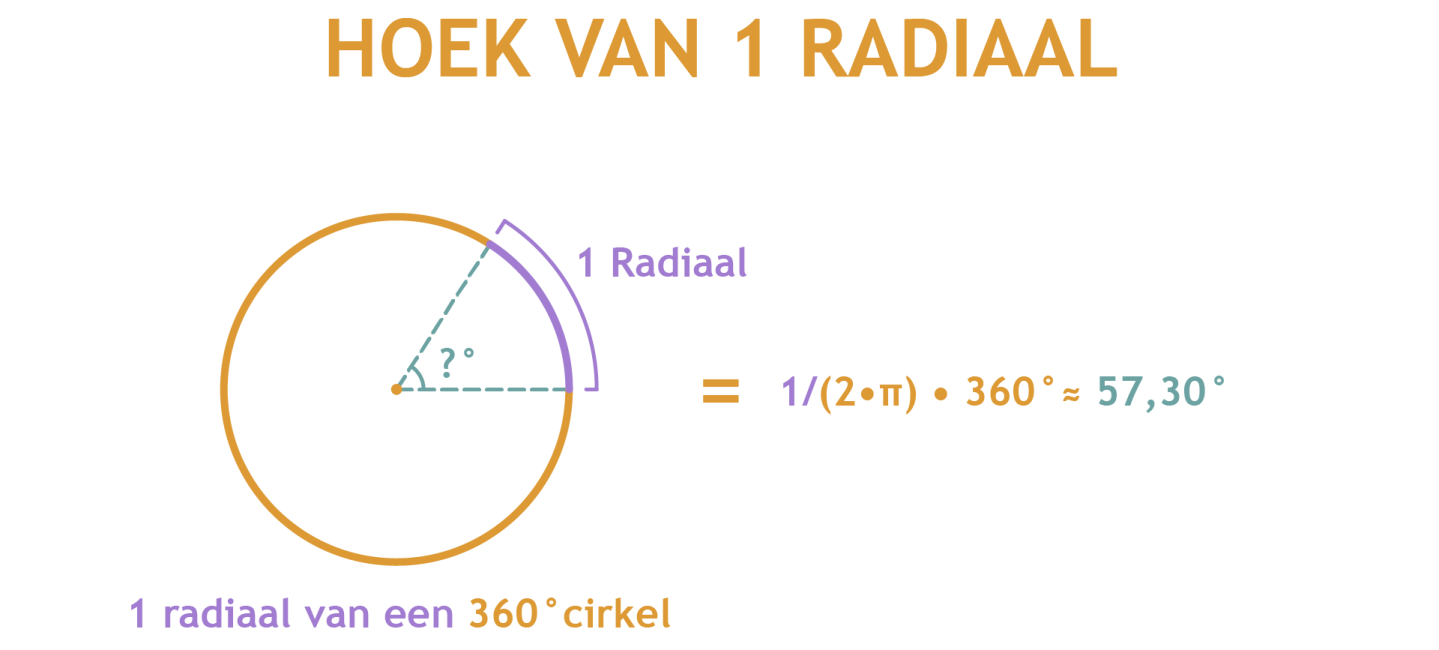
Dit kan ook nog een beetje simpeler berekent worden. In plaats van 1/2π deel te berekenen van een volledige cirkel, kun je ook 1/π deel van een halve cirkel van 180° berekenen. Wanneer we nu de hoek van een radiaal berekenen krijgen we de formule: 1/π•180°.
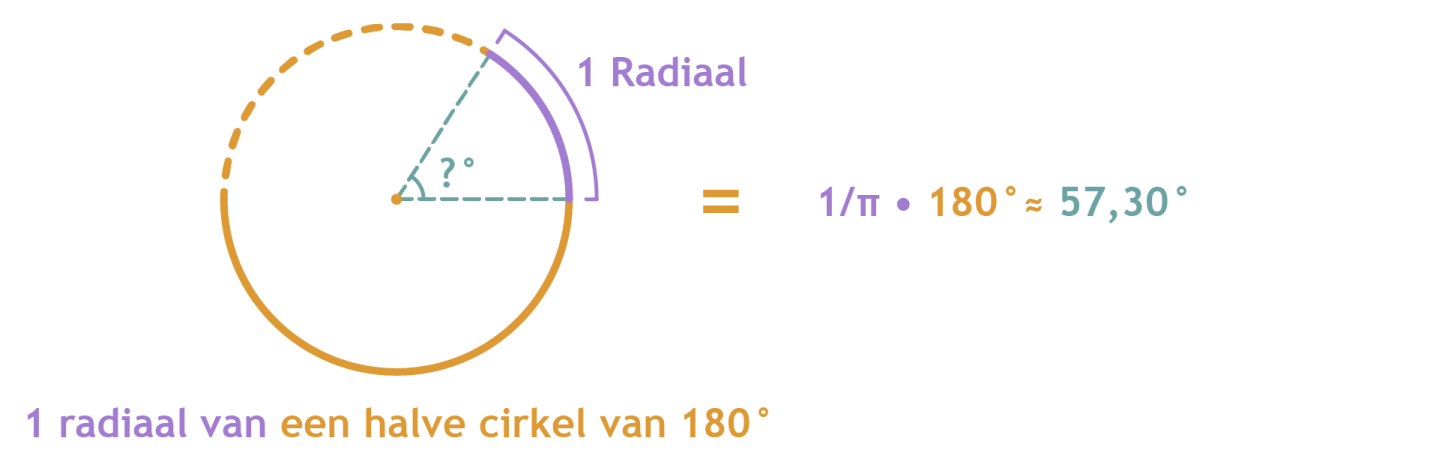
Dit werkt hetzelfde als je bijvoorbeeld de hoek van 4/10π radialen wilt berekenen. 4/10π is eigenlijk 4/10 deel van π. We weten nu dat π gelijk is aan 180°. Dus wat we willen berekenen is 4/10 deel van 180°. Dan krijgen we de formule: 4/10•180°. Dit geeft als oplossing 72°.
7. Samengevat
De grootte van een hoek van 1 radiaal is dus afgerond 57,30°. De grootte van deze hoek wordt bij wiskunde gebruikt als hoekmaat. Deze hoekmaat noemen we een radiaal. Dus wanneer er over een radiaal wordt gesproken, wordt er een hoek van afgerond 57,30° mee bedoeld. De afkorting van een radiaal is “rad”. P.S. “π rad” spreek je niet uit als “piraat”. 😉
Bij een radiaal is de verhouding tussen de cirkelboog en de straal altijd gelijk, omdat de lengte van de cirkelboog van een radiaal gelijk is aan de straal. Dit betekent dat een cirkel altijd 2π radialen bevat en dat de hoek van een radiaal altijd afgerond 57,30° is. Bij elke cirkel met wat voor afmeting dan ook.
In het kort is een radiaal dus een cirkelboog met een lengte die gelijk is aan de lengte van de straal. En een radiaal heeft altijd een hoek van afgerond 57,30°.
8. Formules
Van graden naar π rad:
45° = 45/180°•π = 1/4•π rad
Van π rad naar graden:
0,5π rad = 0,5•180° = 90°
Van decimale rad naar graden:
1,5 rad = 1,5•(180°/π) ≈ 86°
Van graden naar decimale rad:
86° = 86/180°•π ≈ 1,5 rad
This Post Has 2 Comments
- Hairstyles September 3, 2019 Reply
Keep working ,terrific job!
- Haider Bassim May 7, 2021 Reply
Jarnu Wouda your blog is still helping people, thanks for this magnificent work ❤❤


This Post Has 2 Comments
Keep working ,terrific job!
Jarnu Wouda your blog is still helping people, thanks for this magnificent work ❤❤